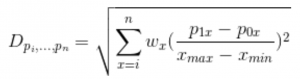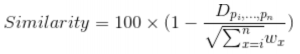Editor’s note: This is a guest post written by Emmanuel Perry. Manny recently created a Shiny app for calculating statistical similarities between NHL players using data from www.war-on-ice.com. The app can be found here. You can reach out to Manny on Twitter, @MannyElk.
We encourage others interested in the analysis of hockey data to follow Manny’s lead and create interesting apps for www.war-on-ice.com.
The wheels of this project were set in motion when I began toying around with a number of methods for visualizing hockey players’ stats. One idea that made the cut involved plotting all regular skaters since the 2005-2006 season and separating forwards and defensemen by two measures (typically Rel CF% and P/60 at 5v5). I could then show the position of a particular skater on the graph, and more interestingly, generate a list of the skaters closest to that position. These would be the player’s closest statistical comparables according to the two dimensions chosen. Here’s an example of what that looked like:
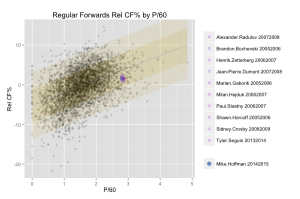
(click to enlarge)
The method I used to identify the points closest to a given player’s position was simply to take the shortest distances as calculated by the Pythagorean theorem. This method worked fine for two variables, but the real fun begins when you expand to four or more.
In order to generalize the player similarity calculation for n-dimensional space, we need to work in the Euclidean realm. Euclidean space is an abstraction of the physical space we’re familiar with, and is defined by a set of rules. Abiding by these rules can allow us to derive a function for “distance,” which is analogous to the one used above. In simple terms, we’re calculating the distance between two points in imaginary space, where the n dimensions are given by the measures by which we’ve chosen to compare players. With help from @xtos__ and @IneffectiveMath, I came up with the following distance function:
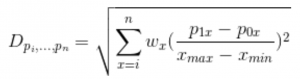
And Similarity calculation:
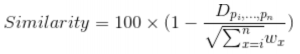
In decimal form, Similarity is the distance between the two points in Euclidean n-space divided by the maximum allowable distance for that function, subtracted from one. The expression in the denominator of the Similarity formula is derived from assuming the distance between both points is equal to the difference between the maximum and minimum recorded values for each measure used. The nature of the Similarity equation means that a 98% similarity between players indicates the “distance” between them is 2% of what the maximum allowable distance is.
To understand how large the maximum distance is, imagine two hypothetical player-seasons. The highest recorded values since 2005 for each measure used belong to the first player-season; the lowest recorded values all belong to the second. The distance between these two players is the maximum allowable distance.
Stylistic similarities between players are not directly taken into account, but can be implicit in the players’ statistics. Contextual factors such as strength of team/teammates and other usage indicators can be included in the similarity calculation, but are given zero weight in the default calculation. In addition, the role played by luck is ignored.
The Statistical Similarity Calculator uses this calculation to return a list of the closest comparables to a given player-season, given some weights assigned to a set of statistical measures. It should be noted that the app will never return a player-season belonging to the chosen player, except of course the top row for comparison’s sake.
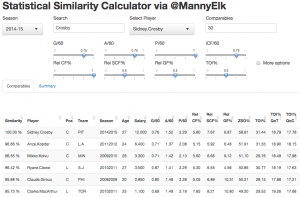
(click to enlarge)
Under “Summary,” you will find a second table displaying the chosen player’s stats, the average stats for the n closest comparables, and the difference between them.
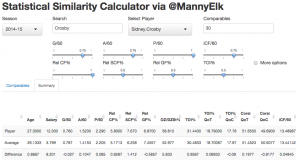
(click to enlarge)
This tool can be used to compare the deployment and usage between players who achieved similar production, or the difference between a player’s possession stats and those of others who played in similar situations. You may also find use in evaluating the average salary earned by players who statistically resemble another. I’ll continue to look for new ways to use this tool, and I hope you will as well.
** Many thanks to Andrew, Sam, and Alexandra of WAR On Ice for their help, their data, and their willingness to host the app on their site. **